Definición de Triangulo equilátero

A instancias de la Geometría, un triángulo es aquel polígono que se encuentra conformado por tres rectas, las cuales se cortan dos a dos en tres puntos no alineados.
En un triángulo, aquellos puntos en los que las rectas se encuentran se conocen como vértices, en tanto, los lados del mismo serán cada segmento de recta, y por su parte, la unión de dos lados termina conformando los ángulos interiores del triángulo en cuestión.
De lo expuesto, entonces, obtendremos las características físicas salientes de esta figura plana, que son: tres ángulos internos, tres externos, también tres vértices y tres lados.

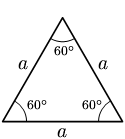
Ahora bien, existen diferentes tipos de triángulos, en tanto, en relación a la longitud de sus lados nos encontramos con el triángulo equilátero, que es aquel que nos ocupará a continuación y que se caracteriza por presentar los tres lados del mismo tamaño, cuestión por la cual además resultan ser equiangulares, o sea, sus tres ángulos internos presentarán la misma medida, que en este caso es de 60°.

La construcción de este tipo de triángulo es plausible de hacerla a partir de la utilización de una regla y de un compás, instrumentos éstos básicos y muy utilizados en esta materia para trazar rectas, ángulos, entre otros.
En el caso del triángulo equilátero es bastante sencillo el proceso de trazado, primero, se deberá trazar una circunferencia, acto seguido el compás deberá abrirse en la media de 120°, luego se marcarán tres puntos, cada uno respetando la misma distancia y finalmente se unen los puntos trazados.

Cabe destacarse que esta figura geométrica ha estado desde siempre muy presente en la vida del hombre, ya que aparece en muchas de las construcciones realizadas por este. El sitio arqueológico bautizado como Lepenski Vir, en Serbia, un asentamiento prehistórico que ostenta alrededor de ocho mil años de antigüedad. La mencionada fue una civilización ciertamente avanzada que ya por aquel tiempo dominaba materias como el urbanismo, la arquitectura, la matemática, la astronomía y la geometría.